Uji Hipotesis t-test dengan menggunakan Microsoft Excel – Microsoft Excel sebagai aktivitas aplikasi spreadsheet yang sangat terkenal ini juga mempunyai kemampunan untuk melaksanakan Analisis Statistik uji hipotesis, baik Uji Hipotesis dalam bentuk t test maupun z test. Dengan Install Add-Ins Anaysis Toolpak ke dalam Microsoft Excel, melaksanakan Uji Hipotesis di Microsoft Excel menjadi pekerjaan yang sangat gampang sekali.
Terdapat beberapa jenis Uji t test yang sanggup dilakukan oleh Add-Ins Analysis Toolpak Microsoft Excel antara lain :
- t-test : Paired Two Sample for Means, yaitu t-test yang dipakai untuk menguji perbedaan rata-rata (mean) 2 Variabel dari sampel yang sama.
- t-test : Two-sample Assuming Equal Variances, yaitu t-test yang dipakai untuk menguji perbedaan rata-rata (mean) 2 variabel dari sampel yang berbeda dengan meng-asumsi-kan kedua sampel tersebut mempunyai variance yang sama.
- t-test : Two-sample Assuming Unequal Variances, yaitu t-test yang dipakai untuk menguji perbedaan rata-rata (mean) 2 variabel dari sampel yang berbeda dengan meng-asumsi-kan kedua sampel tersebut mempunyai variance yang tidak sama.
Contoh Kasus Uji Hipotesis t-test dengan Menggunakan Microsoft Excel
Berikut ini yakni Contoh masalah dan cara melaksanakan uji t-test dengan menggunakan Microsoft Excel :
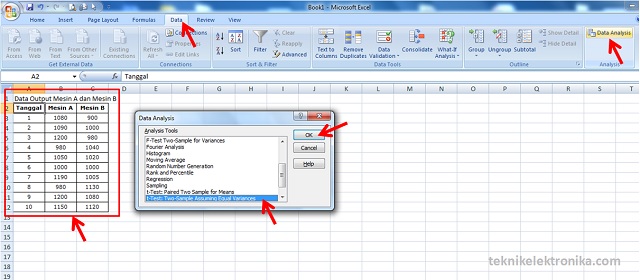
Seorang Manager Engineering ingin melaksanakan penelitian terhadap 2 merek mesin produksi untuk mengetahui apakah Mesin Merek A menghasilkan Output yang lebih banyak dari Mesin B. Oleh alasannya itu, Manager Engineering tersebut kemudian mengambil data sebanyak 10 hari kerja dengan perkiraan variasi output dari kedua mesin tersebut yakni sama. Berikut ini yakni Tabel Output yang dihasilkan oleh kedua mesin tersebut :
Penyelesaian (Menggunakan t-test : Two sample Assuming Equal Variances)
Hipotesis :
H0 : µ1 ≤ µ2 (Output Mesin Merek A dan Mesin Merek B yakni sama atau lebih sedikit)
H1 : µ1 > µ2 (Output Mesin Merek A lebih banyak dari Mesin B)
Tentukan Significance Level
α = 5% atau 0.05
Kriteria penerimaan Uji Hipotesis :
Terima H0 jikalau t hitung ≤ t tabel atau p-value > alpha (α)
Tolak H0 Jika t hitung> t tabel atau p-value ≤ alpha (α)
Cara Analisis Data dengan menggunakan Microsoft Excel
- Buka Program Microsoft Excel.
- Masukkan data yang telah didapat ke dalam Worksheet Excel.
- Di Menu Bar, Klik [Data].
- Klik [Data Analysis] pada Menu Bar Data, maka akan muncul Window “Data Analysis” menyerupai dibawah ini :
- Pilih [t-test : Two-sample Assuming Equal Variances].
- Klik [OK], maka akan muncul Window “t-test : Two-sample Assuming Equal Variances”.
- Pada Kotak Variable 1 Range, Klik tombol “selection” untuk seleksi atau blok tempat data yang akan dianalisis (B2:B12) atau ketikan langsung $B$2:$B$12 kedalam Kotak Variable 1 Range.
- Pada Kotak Variable 2 Range, Klik tombol “selection” untuk seleksi atau blok tempat data yang akan dianalisis (C2:C12) atau ketikan langsung $C$2:$C$12 kedalam Kotak Variable 1 Range.
- Pada Kotak “Hypothesized Mean Difference”, isikan 0 didalamnya dengan perkiraan tidak ada perbedaaan rata-rata antara mesin merek A dan mesin merek B.
- Berikan centang pada “Label” untuk menawarkan keterangan pada tabel hasil analisis.
- Pada Kotak “Alpha”, isi 0.05 yaitu significance Level yang kita tentukan sebelumnya yaitu 5%.
- Pada “Output Option” pilih “New Worksheet Ply” kemudian isikan “Analisis Uji t test A dan B”. Langkah ini untuk menempatkan hasil analisis ke worksheet gres dengan nama “AnalisisUji t test A dan B” tetapi masih dalam Workbook atau file yang sama.
Perlu diingat : Penamaan Worksheet dihentikan melebihi 31 huruf dan dihentikan menggunakan simbol menyerupai “-, +, /, *” atau simbol-simbol lainnya. - Klik [OK].
- Maka Hasil Analisis Statistik Uji Hipotesis t-test dengan membandingkan 2 rata-rata sampel akan muncul di Worksheet gres yang berjudul “Analisis Uji t test A dan B”.
Interpretasi Hasil Analisis Statistik Uji Hipotesis t-test
- Mean adalah nilai rata-rata Output Mesin Merek A = 1092 dan nilai rata-rata Output Mesin Merek B = 1027.5
- Variance adalah nilai variasi Output Mesin Merek A = 7973.333 dan nilai variasi Output Mesin Merek B = 4729.167
- Observations adalah jumlah pengamatan Mesin Merek A dan Mesin Merek B yang masing-masing berjumlah 10 pengamatan.
- Pooled Variance yakni variasi adonan Mesin Merek A danMesin Merek B yaitu 6351.25
- Hypothesized Mean Difference yakni perbedaan rata-rata antara MesinMerek A dengan Mesin Merek B, tetapi untuk teladan masalah ini, kita asumsikan tidak ada perbedaan sehingga nilainya yakni “0” (lihat langkah 9 diatas).
- df adalah Degree of Freedom atau derajat kebebasan yang diperoleh melalui perhitungan n1 + n2 – 2 sehingga 10 + 10 – 2 = 1.
- t-stat adalah nilai t hitung yaitu sebesar 1.809.
- P(T<=t) one tail adalah p-value yaitu sebesar 0.043.
- t critical one tail adalah nilai t tabel yaitu 1,734.
Keterangan :
- Karena hipotesis-nya mengambarkan satu arah yaitu µ1 > µ2 (lebih besar), maka yang dilihat hanya p-value dan t tabel (t critical) satu arah saja yaitu ONE TAIL.
- Untuk Contoh Kasus ini, jangan melihat hasil yang bertuliskan TWO TAIL.
- Kita sanggup menggunakan kritereia penerimaan p-value ataupun t hitung (boleh hanya menggunakan salah satunya saja).
KesimpulanStatistik :
Dari Hasil Analisis Statistik Uji Hipotesis t-test di atas, kita sanggup menyimpulkan sebagai berikut :
t hitung (1.809) > t tabel (1.734) berarti kita menolak H0 (TERIMA H1)
atau
p-value (0.045) < alpha (0.05) berarti kita menolak H0 (TERIMA H1)
KesimpulanPraktek :
Dari Hasil Analisis Statistik Uji Hipotesis t-test diatas, kita menyimpulkan Mesin Merek A menghasilkan Output yang lebih banyak dari Mesin Merek B.
Untuk lebih Jelas mengenai Uji Hipotesis dan Rumus Perhitungan serta Kriteria Penerimaannya, anda sanggup mengunjungi Artikel : Uji Hipotesis (Hypothesis Testing).
Dengan demikian, kita sanggup menggunakan Microsoft Excel dalam melaksanakan Uji Hipotesis sehingga pekerjaan Analisis Statistik menjadi lebih gampang tanpa melaksanakan perhitungan melalui rumus yang rumit dan rawan akan kesalahan hitung. Tetapi sebelumnya, anda harus Install Add-Ins Analysis Toolpak ke Microsoft Excel untuk sanggup melaksanakan Uji Hipotesis atau Analisis Statistik lainnya. Anda sanggup mengunjungi Artikel : Cara Install Add-Ins Analysis Toolpak Microsoft Excel untuk mengetahui cara instalasinya. Analysis Toolpak merupakan Add-Ins gratis bawaan Microsoft Excel 2007.
Sumber https://teknikelektronika.com/